Torna alla panoramica
Sample Division as a Basis for Modern Analytical Methods
The problem
Instruments used to measure particle size have now achieved a degree of accuracy which was inconceivable years ago. Tolerances are constantly being reduced and the latest versions on the market operate faster and more accurately than their predecessors. The introduction of software graphics coupled with multitasking operating systems together with ever more powerful computers has led to higher reliability and reproducibility than ever before. The results obtained in this way can be trusted.
That’s the theory. But in practice the situation is sometimes a little more complex. Although the analysis promises accuracy and precision, maverick results inexplicably occur which raise doubts about the highly praised instruments which promise so much. But the true reason for the anomalous results is not in the testing process with a floating decimal point or operator error; it is simply due to the protocol of the preparation of the samples before they are presented to the measuring system.
It is an amazing fact that the market for high precision fully automatic analysers is constantly growing, whilst no-one seems to be concerned about the preparation and collecting of the samples, factors which are equally if not more important in obtaining a reliable result. Enlightenment on the aspect of particle size has improved as higher levels of accuracy have been achieved1.The emphasis has now shifted to the sample preparation aspect of the measuring process.
The task at hand
The practical use of expensive, high-quality analysers is directly related to the sample presented for analysis. The analysis error always includes both sampling and measuring errors. Based on the law of error propagation, the ascertained total error in the value of the results is2
S tot =√ s 2 measurement + s 2 sample
The standard deviation of the value of the results in terms of the analysed material is determined by the analysers to a significant extent only if the variance for the sample preparation is markedly less than the variance of the analysers. Therefore the results are only reproducible if the sample to be analysed is fully representative of the material to be tested.
In this context, "representative" is generally understood to mean that the samples taken can be equated with the entire batch a priori. If the mixture state of the original sample is described by a property function, the sampling is representative if the measured values distributed over the location adequately approximates the property function3.
If a number of individual samples are taken from a well-mixed whole, its composition is subject to a statistic fluctuation insofar as a specific feature is concerned. An error can result because a sample is taken from a segregated basic quantity and always occurs in this case, since mixtures are never ideal. To minimize the errors, as many small samples as possible must therefore be taken from random locations in the basic whole and then combined.
The solution
Usually, the sample available to the laboratory may be 2000 g whereas the quantity used for analysis is less than 200 mg. So we have to have an accurate method of sub dividing the lab sample so that the trial 200 mg used for analysis is fully representative of the original. This is the ideal situation and can only be achieved with an accurate sample divider. Whether division is in one or more steps, it has no relevancy over error preparation only on the costs of the additional cleaning processes.
The FRITSCH Rotary Cone Sample Divider LABORETTE 27 is therefore available with a division ratio of 1:30 among others. This makes it possible to divide total samples of up to 300 ml into 30 individual samples in one step. Also, dividing cones with ratios of 1:8 or 1:10 are available in different materials so that they can be matched to different types of samples.
The patented design is based on the combination of 3 division methods within a single instrument. The sample is fed onto a dividing cone via a hopper. The dividing cone is designed to emulate the process of „Coning & Quartering“ which is acknowledged as being the most accurate technique for sample division. The entire system rotates and the sample material is accelerated outwards so that it is transferred into the guide channels ensuring that as many as 30 individual samples are collected. The rotation of the dividing cone increases the number of divisions to up to 2,600 per minute; hence the ultimate sample is composed of a very large number of individual samples.
The results
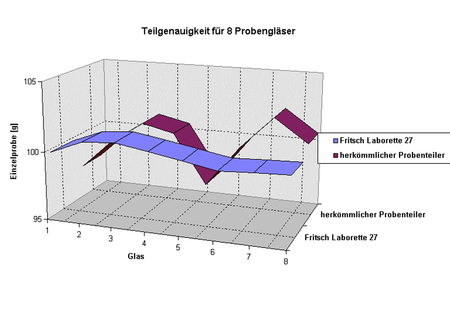
A mixture consisting of about 800 g of quartz sand was created and divided. Figure 1 compares the FRITSCH Rotary Cone Sample Divider with a rotary sample divider with local feeding directly over the sample containers. To attain the same ratios, the dividing cone for eight 500 ml sample containers was used. A check of equal division of samples to the sample containers showed that the LABORETTE 27 is clearly superior to conventional sample dividers.
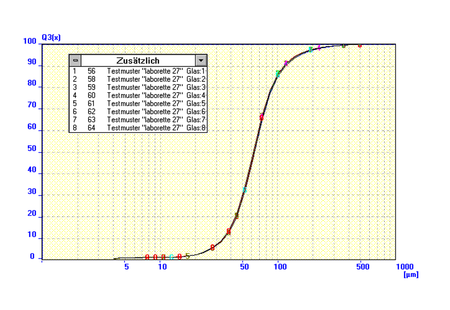
Figure 2 below shows no significant differences in the particle size distribution for each receiver. The deviations per sample are very small. The analysis was conducted with the FRITSCH Particle Sizer ANALYSETTE 22.
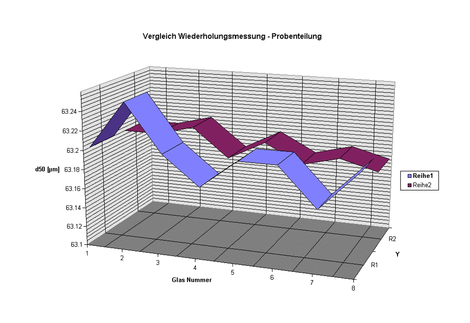
Figure 4 below, shows the median values of particle size distribution in the individual sample containers in series 1, whereas 8 reproducibility measurements of the same material are plotted in series 2 with no change in the instrument parameters.
The median average of the 8 reproducibility measurements is x = 63.1925 ± 0.012 [μm], whereas the median average of the individually measured samples in the 8 sample containers is x = 63.1975 ± 0.027 [μm]. The comparison illustrates that the accuracy of the analyser is naturally considerably higher than the accuracy after sample division. Nevertheless, it is clearly evident that the systematic error caused by the LABORETTE 27 is very small indeed.
Conclusions
The dividing accuracy exerts a decisive influence on the precision of a feature analysis. It can be minimized through design measures. FRITSCH succeeded here with the LABORETTE 27: this rotary cone sample divider enables modern analysers to fully exploit their capabilities. The LABORETTE 27 should stand side-by-side with every modern analyser.
-
Download the FRITSCH-report as PDF file
-
Sources and continuative Literature:
[1] Dipl.-Phys. Götz von Bernuth, "Probenvorbereitung", Kontrolle, September 1984
[2] Dr.-Ing. H. Müller, Dr.-Ing. D. Espig, Ing. S. Kauter, "Probenvorbereitung auf wissenschaftlicher Grundlage", Aufbereitungstechnik, 8/1986.
[3] Prof. Dr.-Ing. Karl Sommer, "Seminar Fritsch Probennahme", Mannheim, Germany, June 28, 1995
Torna alla panoramica